聯(lián)系我們
- 上海耐創(chuàng)測試技術(shù)有限公司
- 聯(lián)系人:陳工
- 電話:021-39197548
- 郵箱:zhujing@forcechina.com?
- 地址:上海市嘉定區(qū)馬陸鎮(zhèn)寶安公路2999弄東方慧谷50號2層

基于矩陣補償方法的串擾修正
文章出處:NaiChuang人氣:發(fā)表時間:2021-06-18 14:28:21
基于矩陣補償方法的串擾修正
美國SDI公司 David Schrand
力/力矩傳感器設(shè)計用于【沿著定義的軸向,通常標記為X,Y和Z】測量力和力矩。這些力/力矩傳感器由1~6個通道;6通道的力/力矩傳感器包含三個通道的力Fx,Fy,Fz和三個通道的力矩Mx,My,Mz;
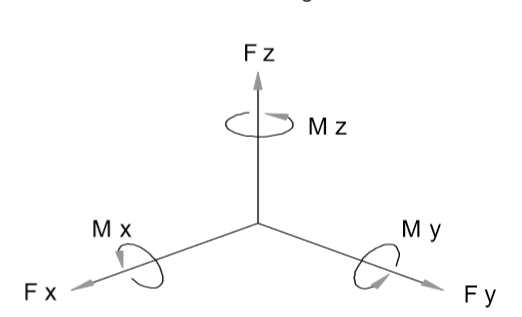
理想狀態(tài)是,一個測量軸上的負載將不會在其它任何測量通道上產(chǎn)生輸出。
現(xiàn)實是,沒有任何多軸向傳感器可以做到這種互不干擾;
對于大多數(shù)的多通道傳感器而言,這種不需要的輸出,我們稱之為串擾,一般在1%~5%之間;雖然1%~5%的串擾聽起來不多,但是對于有六個通道的力/力矩傳感器而言,每一個通道都會有來自其它五個通道的串擾,這種串擾疊加在一起就可能造成5%~25%的串擾輸出;
基本上,有兩種辦法來減少由多通道之間的串擾帶來的測量誤差:
第一種方法是在傳感器后端加補償電路和對傳感器機械結(jié)構(gòu)進行改良,以求達到減小【非測量軸的外來負載引起的通道輸出】;這種方法雖然有效,但是如果要補償兩個通道以上的外部負載,這種方法是耗時且不切實際的;
第二種是通過數(shù)學(xué)方法,對各個軸向的負載輸出進行解析校準來得出正確的通道輸出值,這種方法對于任何數(shù)量的外部載荷都是有效的,并且可以通過應(yīng)用“交叉耦合系數(shù)”或逆矩陣方法來表征為數(shù)學(xué)串擾補償。
我們將要講的就是矩陣系數(shù)方法。
當負載施加到力傳感器時,與該負載對應(yīng)的測量通道將響應(yīng)輸出。然而,如前所述,與施加的負載軸向不一致的其他測量通道也將對該負載做出響應(yīng)。這是壞消息,好消息是,對于任何給定的負載或負載組合,該響應(yīng)是可重復(fù)的。這意味著通過在校準過程中仔細地應(yīng)用這些無關(guān)的負載,并記錄每個通道輸出響應(yīng)到這些負載,可以創(chuàng)建傳感器的輸出輪廓。
從這里,可以創(chuàng)建一系列聯(lián)立方程來描述力傳感器的串擾性能。通過使用來自傳感器的所有通道的任何一組同時數(shù)據(jù)來求解該系列方程,可以確定產(chǎn)生該唯一數(shù)據(jù)集的真實負載條件。該方法的缺點在于,需要加載標定傳感器的所有軸向。這通常不是問題,因為在大多數(shù)情況下,我們可以在加載的同時用數(shù)據(jù)采集設(shè)備監(jiān)測每一個通道的輸出。
OFx = K1 ·Fx
同時,其他五個通道的輸出將被記錄為串擾輸出。現(xiàn)在傳感器的傳遞功能開始形成。
OFx = K1·Fx
OFy = K7·Fx
OFz = K13·Fx
OMx = K19·Fx
OMy = K25·Fx
OMz = K31·Fx
通過這一組方程,可以通過將傳感器輸出除以施加的負載來確定每個軸的傳遞函數(shù)(K1,K7等)。
將使用相同的過程來校準傳感器的剩余五個軸,提供剩余的傳遞函數(shù)。 使用疊加理論,可以組合產(chǎn)生完全描述傳感器對所有施加載荷的輸出的輸出方程。
OFx = K1·Fx + K2·Fy + K3·Fz + K4·Mx + K5·My + K6·Mz
OFy = K7·Fx + K8·Fy + K9·Fz + K10·Mx + K11·My + K12·Mz
OFz = K13·Fx + K14·Fy + K15·Fz + K16·Mx + K17·My + K18·Mz
OMx = K19·Fx + K20·Fy + K21·Fz + K22·Mx + K23·My + K24·Mz
OMy = K25·Fx + K26·Fy + K27·Fz + K28·Mx + K29·My + K30·Mz
OMz = K31·Fx + K32·Fy + K33·Fz + K34·Mx + K35·My + K36·Mz
這些方程式描述了傳感器在施加的載荷方面的輸出。 然而,在應(yīng)用中,負載是未知數(shù),輸出是已知的測量量。 利用這六個方程及其六個未知數(shù)(載荷Fx-z和Mx-z),可以解決未知載荷;
【逆矩陣方法】
可以通過使用所謂的逆矩陣法來解決上述的一系列方程式。反矩陣理論,我們可以參考線性代數(shù)中的逆矩陣求法來取得【K·K-1=E】。實質(zhì)上,這是一種“反轉(zhuǎn)”方程式的技術(shù),使得不再像上述那樣將輸出作為負載的函數(shù),所以負載現(xiàn)在是輸出的功能。
用于糾正或補償由于串擾錯誤導(dǎo)致的傳感器輸出的逆矩陣涉及到收集傳感器上的校準數(shù)據(jù)對外部負載的響應(yīng),并使用它構(gòu)建可用于找到傳感器真實負載條件的矩陣。已經(jīng)經(jīng)過徹底校準的多軸傳感器將已經(jīng)具有提供校準數(shù)據(jù)的這種串擾矩陣。有關(guān)創(chuàng)建此矩陣涉及的步驟的更多信息,請參見附錄B“查找逆矩陣”。
這可能看起來很混亂,但是處理一個非常復(fù)雜的問題是一個非常簡單的方法。例如,我們有一個“不太完美”的傳感器。然而,我們確實提供了傳感器提供的串擾矩陣,如下所示。
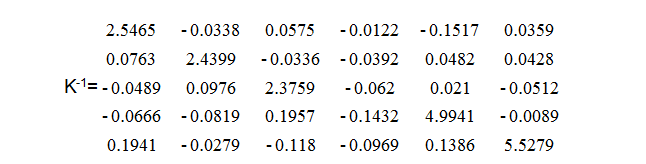
X = K-1·O
使用該逆矩陣,可以計算產(chǎn)生來自傳感器的任何一組同時數(shù)據(jù)的負載。 我們從逆矩陣K-1和方程式開始:
X = K-1·O
或者展開寫:
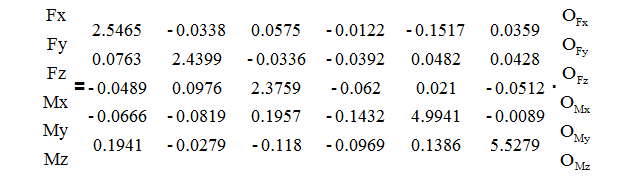
OFx = -1.6510 mV/V OMx = 1.0054 mV/V
OFy = 0.6151 mV/V OMy = 0.8402 mV/V
OFz = 0.2501 mV/V OMz = 0.0067 mV/V
在特定的時間,我們從傳感器獲取以上數(shù)據(jù)
要找到必須存在的Fx負載來創(chuàng)建這六個輸出,我們將逆矩陣的第一行的元素乘以所記錄的各個輸出,并將它們相加:
Fx = (2.5465 * -1.6510) + (-0.0338 * 0.6151) + … + (0.0359 * 0.0067) = -4.35 lb
類似的,可以通過對逆矩陣的剩余五行執(zhí)行相同的操作來計算剩余的五個負載,這樣就能得出一個完整傳感器的加載概況;
Fx = -4.35 lb Mx = 5.54 in lb
Fy = 1.37 lb My = 4.11 in lb
Fz = 0.69 lb Mz = -0.31 in lb
在實際使用中,這些計算可以通過數(shù)據(jù)采集或控制系統(tǒng)實時設(shè)置,也可以通過使用電子表格程序在測試完成后對數(shù)據(jù)進行后處理來完成。 這種技術(shù)通常會將串擾減少到傳感器滿量程的0.5%。
美國SDI公司 David Schrand
力/力矩傳感器設(shè)計用于【沿著定義的軸向,通常標記為X,Y和Z】測量力和力矩。這些力/力矩傳感器由1~6個通道;6通道的力/力矩傳感器包含三個通道的力Fx,Fy,Fz和三個通道的力矩Mx,My,Mz;

理想狀態(tài)是,一個測量軸上的負載將不會在其它任何測量通道上產(chǎn)生輸出。
現(xiàn)實是,沒有任何多軸向傳感器可以做到這種互不干擾;
對于大多數(shù)的多通道傳感器而言,這種不需要的輸出,我們稱之為串擾,一般在1%~5%之間;雖然1%~5%的串擾聽起來不多,但是對于有六個通道的力/力矩傳感器而言,每一個通道都會有來自其它五個通道的串擾,這種串擾疊加在一起就可能造成5%~25%的串擾輸出;
基本上,有兩種辦法來減少由多通道之間的串擾帶來的測量誤差:
第一種方法是在傳感器后端加補償電路和對傳感器機械結(jié)構(gòu)進行改良,以求達到減小【非測量軸的外來負載引起的通道輸出】;這種方法雖然有效,但是如果要補償兩個通道以上的外部負載,這種方法是耗時且不切實際的;
第二種是通過數(shù)學(xué)方法,對各個軸向的負載輸出進行解析校準來得出正確的通道輸出值,這種方法對于任何數(shù)量的外部載荷都是有效的,并且可以通過應(yīng)用“交叉耦合系數(shù)”或逆矩陣方法來表征為數(shù)學(xué)串擾補償。
我們將要講的就是矩陣系數(shù)方法。
當負載施加到力傳感器時,與該負載對應(yīng)的測量通道將響應(yīng)輸出。然而,如前所述,與施加的負載軸向不一致的其他測量通道也將對該負載做出響應(yīng)。這是壞消息,好消息是,對于任何給定的負載或負載組合,該響應(yīng)是可重復(fù)的。這意味著通過在校準過程中仔細地應(yīng)用這些無關(guān)的負載,并記錄每個通道輸出響應(yīng)到這些負載,可以創(chuàng)建傳感器的輸出輪廓。
從這里,可以創(chuàng)建一系列聯(lián)立方程來描述力傳感器的串擾性能。通過使用來自傳感器的所有通道的任何一組同時數(shù)據(jù)來求解該系列方程,可以確定產(chǎn)生該唯一數(shù)據(jù)集的真實負載條件。該方法的缺點在于,需要加載標定傳感器的所有軸向。這通常不是問題,因為在大多數(shù)情況下,我們可以在加載的同時用數(shù)據(jù)采集設(shè)備監(jiān)測每一個通道的輸出。
OFx = K1 ·Fx
同時,其他五個通道的輸出將被記錄為串擾輸出。現(xiàn)在傳感器的傳遞功能開始形成。
OFx = K1·Fx
OFy = K7·Fx
OFz = K13·Fx
OMx = K19·Fx
OMy = K25·Fx
OMz = K31·Fx
通過這一組方程,可以通過將傳感器輸出除以施加的負載來確定每個軸的傳遞函數(shù)(K1,K7等)。
將使用相同的過程來校準傳感器的剩余五個軸,提供剩余的傳遞函數(shù)。 使用疊加理論,可以組合產(chǎn)生完全描述傳感器對所有施加載荷的輸出的輸出方程。
OFx = K1·Fx + K2·Fy + K3·Fz + K4·Mx + K5·My + K6·Mz
OFy = K7·Fx + K8·Fy + K9·Fz + K10·Mx + K11·My + K12·Mz
OFz = K13·Fx + K14·Fy + K15·Fz + K16·Mx + K17·My + K18·Mz
OMx = K19·Fx + K20·Fy + K21·Fz + K22·Mx + K23·My + K24·Mz
OMy = K25·Fx + K26·Fy + K27·Fz + K28·Mx + K29·My + K30·Mz
OMz = K31·Fx + K32·Fy + K33·Fz + K34·Mx + K35·My + K36·Mz
這些方程式描述了傳感器在施加的載荷方面的輸出。 然而,在應(yīng)用中,負載是未知數(shù),輸出是已知的測量量。 利用這六個方程及其六個未知數(shù)(載荷Fx-z和Mx-z),可以解決未知載荷;
【逆矩陣方法】
可以通過使用所謂的逆矩陣法來解決上述的一系列方程式。反矩陣理論,我們可以參考線性代數(shù)中的逆矩陣求法來取得【K·K-1=E】。實質(zhì)上,這是一種“反轉(zhuǎn)”方程式的技術(shù),使得不再像上述那樣將輸出作為負載的函數(shù),所以負載現(xiàn)在是輸出的功能。
用于糾正或補償由于串擾錯誤導(dǎo)致的傳感器輸出的逆矩陣涉及到收集傳感器上的校準數(shù)據(jù)對外部負載的響應(yīng),并使用它構(gòu)建可用于找到傳感器真實負載條件的矩陣。已經(jīng)經(jīng)過徹底校準的多軸傳感器將已經(jīng)具有提供校準數(shù)據(jù)的這種串擾矩陣。有關(guān)創(chuàng)建此矩陣涉及的步驟的更多信息,請參見附錄B“查找逆矩陣”。
這可能看起來很混亂,但是處理一個非常復(fù)雜的問題是一個非常簡單的方法。例如,我們有一個“不太完美”的傳感器。然而,我們確實提供了傳感器提供的串擾矩陣,如下所示。

X = K-1·O
使用該逆矩陣,可以計算產(chǎn)生來自傳感器的任何一組同時數(shù)據(jù)的負載。 我們從逆矩陣K-1和方程式開始:
X = K-1·O
或者展開寫:

OFx = -1.6510 mV/V OMx = 1.0054 mV/V
OFy = 0.6151 mV/V OMy = 0.8402 mV/V
OFz = 0.2501 mV/V OMz = 0.0067 mV/V
在特定的時間,我們從傳感器獲取以上數(shù)據(jù)
要找到必須存在的Fx負載來創(chuàng)建這六個輸出,我們將逆矩陣的第一行的元素乘以所記錄的各個輸出,并將它們相加:
Fx = (2.5465 * -1.6510) + (-0.0338 * 0.6151) + … + (0.0359 * 0.0067) = -4.35 lb
類似的,可以通過對逆矩陣的剩余五行執(zhí)行相同的操作來計算剩余的五個負載,這樣就能得出一個完整傳感器的加載概況;
Fx = -4.35 lb Mx = 5.54 in lb
Fy = 1.37 lb My = 4.11 in lb
Fz = 0.69 lb Mz = -0.31 in lb
在實際使用中,這些計算可以通過數(shù)據(jù)采集或控制系統(tǒng)實時設(shè)置,也可以通過使用電子表格程序在測試完成后對數(shù)據(jù)進行后處理來完成。 這種技術(shù)通常會將串擾減少到傳感器滿量程的0.5%。













 滬公網(wǎng)安備 31011402003414號
滬公網(wǎng)安備 31011402003414號